什麼是代價函數

代價函數的作用是幫助我們找到最佳解的目標函數。代價函數和損失函數有什麼不一樣呢？主要是兩個函數的目標對象不一樣，損失函數是目標範圍定義在單個樣本，算的是一個樣本的誤差。代價函數是定義在整個data-set，取所有樣本誤差的平均值，也就是損失函數的平均值。

代價函數作用原理

對於迴歸問題，我們需要求出代價函數來求解最優解，常用的是平方誤差代價函數。

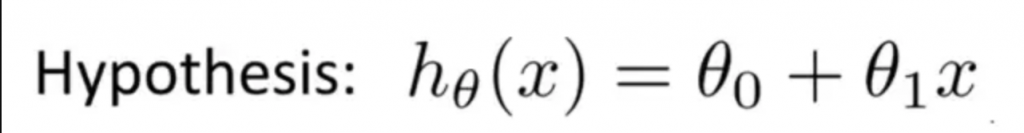
舉例來說，上面的函數有θ0和θ1兩個參數，參數的改變將會導致假設函數產生變化。

現實的迴歸問題裡，數據會以二維圖上點分佈的形式呈現，我們想要解決迴歸問題，就需要找出一條擬合線性方程，換句話說我們想要找出最佳的θ0和θ1參數，使得線性方程的直線可以代表所有數據。

如何找出最佳解呢？這時我們就需要引入代價函數了。以平方誤差函數為例，

假設函數為單一參數方程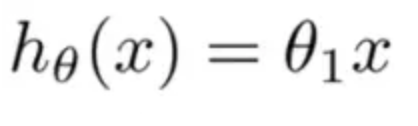

我們將實際數據的值與我們擬合出來的直線的對應值取差值，並且用差值的結果代表擬合結果和真實數據之間的差距。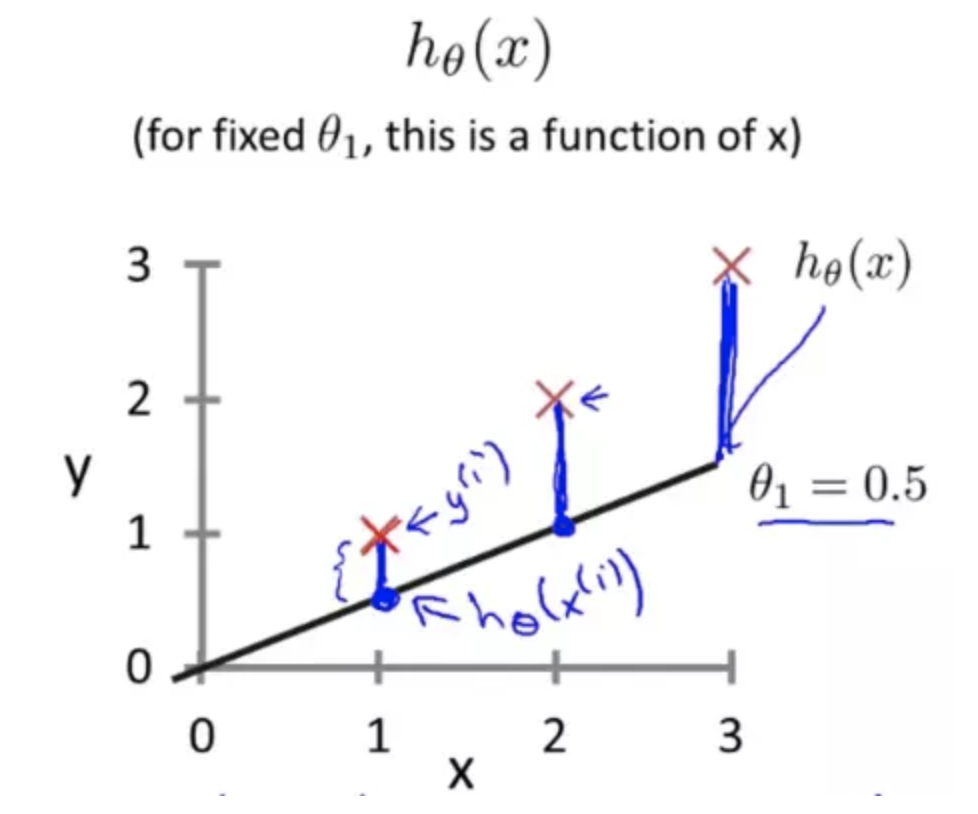

為了不使這個值被極端數據影響，我們採用平方差再取二分之一的方式來減少個別數據的影響，這麼一來我們就得到了代價函數。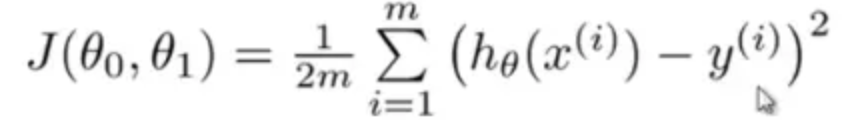

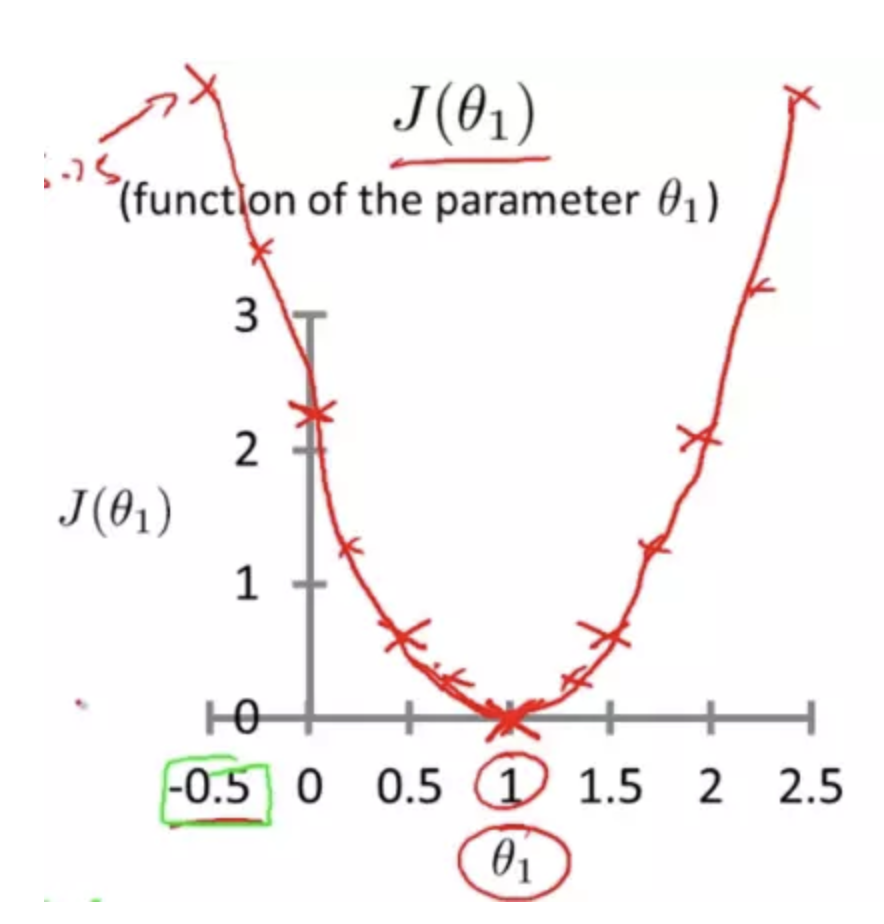
擬合結果的最優解是代價函數的最小值，怎麼証明這個假設呢？
我們將代價函數多次計數的結果做圖，可以看到該代價函數得確存在最小值，在這裡恰好是橫坐標為1的時候。